†Corresponding author. E-mail: hyperchaos@163.com
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11372122 and 11365014).
A nonlinear circuit can be designed by using inductor, resistor, capacitor and other electric devices, and the electromagnetic field energy can be released from the circuit in the oscillating state. The generation of spikes or bursting states in neurons could be energetically a costly process. Based on the Helmholtz’s theorem, a Hamilton energy function is defined to detect the energy shift induced by transition of electric modes in a Hindmarsh–Rose neuron. It is found that the energy storage is dependent on the external forcing, and energy release is associated with the electric mode. As a result, the bursting state and chaotic state could be helpful to release the energy in the neuron quickly.
The neuronal system and biological system consume energy in the metabolic process, so that the neurons can keep normal electric activities.[1– 4] The neuron can give appropriate responses to external forcing, and multiple types of electric modes can be induced due to self-adaption. The dynamics of electrical activities in neuron and collective behaviors for neuronal network have been investigated extensively. For example, bifurcation analysis, pattern selection, and synchronization problem could give reliable investigation for this topic via experimental or numerical ways.[5– 20] For example, Wei and Zuo[5] investigated the chaotic dynamics of the Hindmarsh– Rose neuron by using Shil’ nikov technique. Huang and Hu[10] discussed the plasticity dependence on the pattern dynamics and even the phase transition in neuronal network. Indeed, intelligent circuits are also effective to reproduce the main properties of electrical activities of neurons. For example, some artificial neuronal circuits[21– 23] have been designed to show the electric activities of neurons, but this topic is still open. In a reliable and practical way, the designed neuronal circuits should give a response within smaller transient period under lower power consumption, and the effect of external electromagnetic radiation should be detected as well.
In a neuronal circuit, the energy exchange between electric field and magnetic field can promote the fluctuations of voltage via capacitor and current via inductor. The artificial neuronal circuit driven by external forcing current keeps oscillating when electromagnetic radiation is not considered. A transition of modes in electrical activities can be induced by changing the external forcing current, and these results are similar to the results of biological experiments.[24– 28] The energy release and storage in realistic circuits can be estimated quantificationally, and it is important to detect the energy transmission and release dependences on the electric activity mode in those theoretical neuronal models, which can be verified in PSpice tool and even realistic artificial circuits. The emergence of action potentials represents a fundamental means of signal propagation in the nervous system and it is a metabolically expensive process. In fact, a type of Hamilton statistical function[29– 31] is defined to describe the energy degree in some oscillator model by using Helmholtz’ s theorem, and it was also confirmed in an autonomous circuit composed of inductor, resistor, and capacitor. For example, Shih-Chiung et al.[32] investigated the information entropy and mutual information in discrete movement aiming tasks. Jin et al.[33] reported that a retinal ganglion cell’ s responsiveness change was characterized by reducing firing rate and declining sensitivity during adaptation to high-contrast stimulation; as a result, the system’ s metabolic cost could be saved in the meantime due to the decrease of the neuron’ s firing rate during the adaptation. The neuronal system consists of a large number of neurons with complex connections; signal encoding and action potentials are often associated with energy efficiency, which depends on the characteristics of the input signals, e.g., pulse strength, interpulse intervals, and channel noise.[34, 35] Torrealdea et al.[36] detected the consumption of energy and the information entropy in the signaling activity of a model neuron both when it is supposed to be isolated and when it is coupled to another neuron by an electrical synapse. Furthermore, Moujahid et al.[37] found some conditions under which two non-identical electrically coupled neurons can reach an efficient regime of synchronization at low energy cost by using a defined energy function for a modified Hindmarsh– Rose neuron model with four variables.
The original Hindmarsh– Rose neuron model[38] is reliable to describe the main properties of electrical activities and is available for bifurcation analysis. A four-variable neuron model[7, 39] has been developed from the previous Hindmarsh– Rose neuron model, and more complex dynamical properties can be observed by introducing some new controllable parameters. In Refs. [30] and [37] the Hamilton energy function was calculated, but the energy function seems to be independent of the external forcing, and these results are not consistent with our experimental results, though the differential coefficient of energy function versus time could be dependent on the external forcing. It is worthwhile investigating the energy consumption or cost for neurons during the transition of action potentials and information encoding.[40– 42] In this paper, we argue that appropriate Hamilton energy function should be renewed and the dependence of energy cost on external forcing current should be clarified in a directional way. The new energy function is verified in a realistic circuit, and calculated in the three-variable neuron model under different electrical modes, and the relations between the energy consumption and the action potentials are obtained when the electrical mode is in spiking, bursting or chaotic states, respectively. Furthermore, the transition between different electrical modes in a neuron induced by external forcing will be investigated as well.
A common electric circuit is often composed of inductor, resistor, and capacitor; the schematic diagram is often illustrated as shown in Fig. 1.
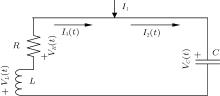 | Fig. 1. Schematic diagram for coupled circuit composed of inductor, resistor, and capacitor where I1 denotes the external forcing current. |
According to the Kirchhoff’ s laws and electromagnetic induction theorem, the equations for the circuit shown in Fig. 1 could be described by
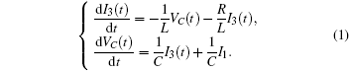
Furthermore, the energy stored in the oscillating circuit can be detected as follows:

which shows some differences from the presentation in Ref. [29], where the effect of external forcing current could not be considered. According to the Helmholtz’ s theorem, it satisfies the criterion as ∇ HTfc = 0, the oscillating circuit can be written as follows:

As a result, it confirms that
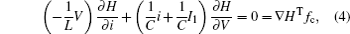

Based on scale transformation, the circuit equation (1) can be described by some equivalent dimensionless dynamical equations as follows:

where 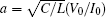
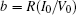
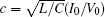
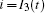
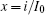
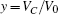
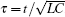

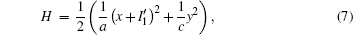
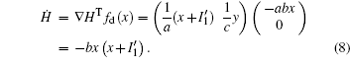
That is to say, appropriate Hamilton function can still be approached and confirmed to find the statistical properties of the dimensionless dynamical models. To ascertain the energy cost in neuronal activity and dependence on action potential, the three-variable Hindmarsh– Rose neuron will be investigated as an example, and the energy fluctuation in an isolated neuron will be detected by changing the external forcing current. The potential mechanism for transition from spiking to bursting state will be investigated, and it could be associated with the energy release. The three-variable Hindmarsh– Rose neuron[38] model is often described by
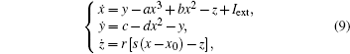
where x, y, z often represents the membrane potential, recovery variable associated with sodium and potassium current, and slow adaption current associated with calcium current, respectively. The parameters are often selected to be a = 1.0, b = 3.0, c = 1.0, d = 5.0, r = 0.006, s = 4.0, and x0 = − 1.56, and the external forcing current Iext is controllable.
According to Refs. [31] and [36] and Helmholtz’ s theorem, [43] the dynamical equations for a neuron are treated as a velocity vector field, and further considered as a sum of two vector fields f(* ) = fc(* ) + fd(* ), where fc(* ) is conservative field containing the full rotation and fd(* ) is dissipative containing the divergence.[43] The two sub-vector fields can be described as follows:
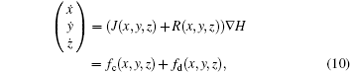
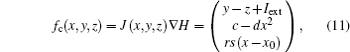

where J(* ) is a skew symmetric matrix that satisfies Jacobi’ s closure condition, as a result, the Hamilton function associated with Eqs. (10) and (9) can be calculated by


By substituting Eqs. (10) and (11) into Eq. (13a), the resulting equation is obtained as follows:

A general solution of Eq. (14) is

and its differential coefficient versus time is calculated from

As a result, the Hamilton energy function as shown in Eq. (15) is a reliable solution of Eq. (14) and satisfies the stable criterion defined in Eq. (13). It is found that the energy function in Eq. (15) is dependent on the external forcing Iext while it was concluded in Refs. [31] and [36] that the Hamilton energy function should be independent of the external forcing term. As a result, some puzzles occur in understanding the energy storage in a neuron or circuit driven by external forcing which can input external energy into the system. This problem can be investigated in the Hindmarsh– Rose neuron by finding solutions for J(x, y, z) and R(x, y, z), and it reads ẋ = (J(x, y, z) + R(x, y, z))∇ H, and we have
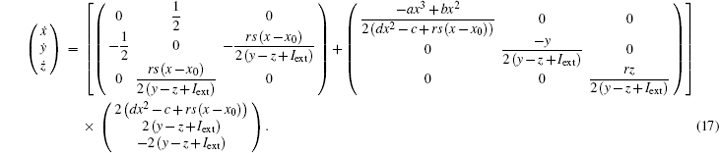
It is confirmed that a new solution for energy function shown in Eq. (15) is reliable as well, and the fluctuation of energy function associated with external forcing is also considered in detail. The modified energy function could be more reliable than the previous energy function in Refs. [31] and [36] so it can be understood that the dependence of energy release on external forcing and action potential is different in a different mode.
In this section, numerical studies are carried out by using the fourth-order Runge– Kutta algorithm with time step h = 0.01, transient period about 2000 time units, and the initial values are selected to be (– 1.31742, − 7.67799, 1.13032). At first, the bifurcation diagram for interspike interval (ISI) versus external forcing current is reproduced in a numerical way, and the results are shown in Fig. 2. Furthermore, the average value for Hamilton energy function is calculated in a transient period (T) range of 1000– 2000, and some statistical properties are detected.
The average Hamilton energy is calculated by defining


where T is the calculation period about 1000 time units and t0 is the beginning time to calculate the average energy function. The energy function and its differential coefficient versus time are described by Eqs. (15) and (16). By changing the external forcing, the evolution of average energy function is plotted in Fig. 3.
 | Fig. 3. Development of average energy function in Hindmarsh– Rose neuron, calculated by changing the external forcing current, and the average time for the calculations T = 1000 time units. |
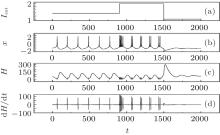
It is found that the average energy in the Hindmarsh– Rose neuron decreases greatly with increasing the external forcing current, and the fluctuation velocity decreases as well. Extensive numerical results confirm that the statistical properties of average energy are greatly independent of the selection of calculation time T. It is important to investigate the relation between the energy function and the action potential. To our knowledge, the Hindmarsh– Rose neuron can undergo spiking state and step into bursting even chaotic state under an action potential, and it may indicate that discharge with high rhythm makes each action potential hold low energy unit. To detect the effect of external forcing on the energy function, the external forcing current is changed with a quick shift, and the results are plotted in Fig. 4.
The results in Fig. 4 confirm that the energy function in the Hindmarsh– Rose neuron is greatly associated with the action potentials, and also dependent on the discharge mode. In the case of spiking state, the energy function fluctuates with higher amplitude than in the case of bursting state. The energy function undergoes quick shift by reducing its value when its electric activity is switched from spiking state to bursting state, and a rapid jump occurs when its discharge activity is switched from bursting state to quiescent state by reducing the external forcing current. As a result, the energy function is restricted in a small range when its action potential is close to quiescent state. Furthermore, it is important to investigate the dependence of energy function on the bursting state, and the results are shown in Fig. 5.
It is found that the energy function used suffers the rapid shift during the transition from one state to another discharge state. The fluctuation range of energy function decreases when the action potential in chaotic state changes into those in bursting and further spiking state by reducing the external forcing current with a jump. Comparing the results in Figs. 4 and 5, it is concluded that the energy in the neuron is associated with action potential and its discharge rhythm, the energy function decreases to a low value when the electric activity is changed to be in high rhythm because each action potential carries certain energy and follows the law of conservation of energy. The external forcing current on the neuron makes the neuron absorb external energy flow; the generation of action potential is associated with energy release. Owing to the law of conservation of energy, each action potential shares certain energy unit, and the energy unit decreases when the electric activity of neuron is changed to be in high rhythm.
In summary, signal propagation and transmission are dependent on energy supply and cost. It is critical for the neuronal system to keep normal electrical activities by adjusting the metabolic process, that is to say, the action potential and discharge modes of neurons are associated with the energy cost. A statistical Hamilton energy is defined to discern the relation among the action potential, transition of electric activities of neuron, external forcing and the energy cost. It explains why the neurons can give an appropriate response to external forcing which supplies continuous energy for neuron.
By using the Helmholtz’ s theorem, a modified Hamilton energy function is defined to discern the dependence of energy flow on the external forcing current imposed on the Hindmarsh– Rose neuron. The energy function in the neuron shows distinct dependence on external forcing (or action potentials) current and thus the discharge states such as quiescent, spiking, bursting and chaotic states. The energy function undergoes a distinct shift and transition when action potential or discharge state is switched quickly. The energy function per time unit or average energy function over certain transient period often maintains a low value when the electric activity changes with high rhythm because of the law of conservation of energy. The proposed Hamilton energy function shows some improvements more than the previous version because the external forcing effect can be discerned directionally so that the dependence of energy on external forcing could be understood intuitively. It also throws light on the understanding of the information encoding and transition of electric activity with the correlation and dependence of energy cost.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|