†Corresponding author. E-mail: lmchen@iphy.ac.cn
*Project supported by the National Basic Research Program of China (Grant Nos. 2013CBA01501 and 2013CBA01504), the National Key Scientific Instrument and Equipment Development Project of China (Grant No. 2012YQ120047), Chinese Academy of Science Key Program, the National Natural Science of China (Grant Nos. 11135012 and 11375262), and the Project of Shandong Province Higher Educational Science and Technology Program, China (Grant No. J11LA52).
We provide the first report on the harmonics generated by an intense femtosecond vector beam that is normally incident on a solid target. By using 2D particle-in-cell (PIC) codes, we observe the third and the fifth harmonic signals with the same vector structure as the driving beam, and obtain an attosecond vector beam pulse train. We also show that the conversion efficiencies of the third and the fifth harmonics reach their maxima for a plasma density of four times the critical density due to the plasma resonating with the driving force. This method provides a new means of generating intense extreme ultraviolet (XUV) vector beams via ultra-intense laser-driven harmonics.
Recently, the strong-field singular beam[1] has attracted increasing attention owing to its wide potential applications. More specifically, it could potentially be used in the acceleration of electrons, [2– 7] positrons, [8] and protons, [9– 12] and the generation of high-energy twisted photons using high harmonic generation in rare gases, [13, 14] Compton backscattering, [15– 17] and undulator radiation.[18, 19] The typical singular beams include the optical vortex beam with helical phase distribution[20] and the cylindrical polarized vector beam (VB).[21] The radially polarized beam (RPB) and the azimuthally polarized beam (APB) are two typical VBs. Shi et al.[22] proposed the design of a relativistic laser pulse interacting with a spiral-shaped thin foil target and created an ultra-intense optical vortex. We found[23] that the ultra-intense optical vortex possess the evident high-order odd harmonics with high-order TC. Zhang et al.[24] proposed the use of a linearly polarized Laguerre– Gaussian (LG) laser pulse with a helical phase structure to irradiate a solid foil, and obtained intense high-order optical vortices. However, harmonic generation using ultra-intense VB interacting with targets has not been reported.
In this paper, we propose a method for producing ultra-short, intense, ultraviolet VBs by using a VB laser pulse normally incident on a solid target without a damage threshold. We obtain the evident third and fifth VB harmonics, and find that the harmonics have the same vector structure as the driving beam. By filtering the fundamental component of the driving beam, we obtain an attosecond VB pulse train.
The typical VB with the same amplitude distribution as the LG10 (Laguerre– Gaussian mode) can be expressed as
 |
where

In the above equations, C is a constant for normalization, A is the vector potential, c is the speed of light in a vacuum, e is the charge of the electron, me is the mass of the electron, x is the laser propagation direction, and (r, φ ) are the polar coordinates in the y– z plane, wherein φ takes on values from 0 to 2π . The θ is a constant, for which θ = 0 corresponds to an RPB and θ = π /2 corresponds to an APB. The λ 0 is the laser wavelength, k is the wave number, ω 0 is the laser frequency, w0 is the beam waist, f is the Rayleigh length, R(x) is the radius of curvature of the wavefronts, ζ (x) is the Gouy phase of the beam, and t0 is the laser pulse width.
Figures 1(a) and 1(b) show the schematic diagrams of two typical VBs with cylindrically symmetric polarization: an APB and an RPB, respectively. The arrows in Figs. 1(a) and 1(b) represent the directions of polarization. From Figs. 1(a) and 1(b), we can see the APB and RPB are local linearly polarized. For one fixed VB, the sectional views are identical. It is therefore feasible to study a VB that is normally incident on a solid target in a 2D plane. However, in the case of oblique incidence, 2D simulations seem to be insufficient for fully characterizing the asymmetrical sectional view.
 | Fig. 1. Schematic diagrams of (a) an azimuthally polarized beam and (b) a radially polarized beam. (c) The electric field Ez of the APB in the x– y plane. |
We carried out simulations using 2D particle-in-cell (PIC) codes KLAPS (kinetic laser plasma simulation).[25] In the simulation, the intensity distribution expressed by Eq. (1) was used. At first, we took the APB (θ = π /2) with the parameters a0 = 1, t0 = 10T (where T is the laser period), and w0 = 10 μ m to irradiate a solid target with a density of n = 4nC (where nC = 1.74 × 1021 cm− 3 is the critical plasma density for λ 0 = 0.8 μ m). A 4-μ m-thick solid target was adopted. Figure 1(c) shows the s-polarized electric field Ez of the APB in the x– y plane. The upper and lower parts in Fig. 1(c) correspond to φ = 0 and φ = π , respectively.
From the simulation results, we find that the reflected field F(t) is s-polarized, it means that the local reflected field has the same polarization state as the local linearly polarized driving beam in the case of normal incidence.[26] We then calculate the corresponding spectral distribution of the reflected field F(t). Figures 2(a) and 2(b) show the spectral amplitude and phase distributions of the reflected field, respectively. From Fig. 2(a), we can clearly see the third and the fifth harmonics. From Fig. 2(b), we can see that the upper and lower parts of the fundamental, the third, and the fifth harmonics have the opposite phases with respect to each other, which indicates that the third and the fifth harmonics would have the same vector structure as the driving beam. Here we do not take the seventh harmonic into consideration because it is very weak. At the plasma density n = 4nC, there exists a weak signal of even harmonics, which can be explained by the plasma resonating with the frequency of the driving force (laser ponderomotive force).[26] There are no even harmonics signals for other plasma densities. The strong modulation of the fundamental signal results from the interference of the incident laser with the reflected laser, because we set the record plane near the target surface. For obtaining the accurate phase information of the spectrum, we correct the Fourier transform of F(t) with an additional phase factor. The unknown zero time results in the modulated phase spectrum of the third and the fifth harmonics.
For comparison, without changing the laser intensity distribution and other parameters, we use the hollow beam with the same polarization and the same phase normally incident on the solid target. Figure 2(c) shows the corresponding spectral phase distribution of the reflected field, from which we can see that the upper and lower parts have the same phase. The simulation results therefore demonstrate that the third and the fifth harmonics maintain the same vector structure as the driving beam.
The odd harmonics can be well explained by the reflection from the “ oscillating mirror” [26, 27] driven by the laser ponderomotive force. This is because the ponderomotive force of the linearly polarized laser has a double-laser-frequency oscillation component. For the purpose of comparison, we also simulate the case of the circularly polarized beam; in this case, no harmonics are found because the ponderomotive force is quasi-steady.
By removing the component of the fundamental frequency from the reflected field, we obtain an attosecond APB pulse train mainly composed of the third and the fifth APB harmonics. Figures 3(a) and 3(b) represent 2D and 1D intensity distributions of the APB train, respectively. From Fig. 3(b), we measure the temporal period of the adjacent APB pulses to be about 400 as.
 | Fig. 3. (a) The 2D and (b) 1D intensity distributions of the attosecond pulse train obtained in the simulation, where in a0 = 1, t0 = 10T, w0 = 10 μ m, and n = 4nC. |
We study the conversion efficiencies of the third and the fifth harmonics by changing the plasma density n. From Fig. 4(a), we can see that both the third and the fifth harmonics have maximum conversion efficiencies at n = 4nC. For the plasma density n = 4nC, the plasma oscillates with the frequency of the driving force. The resonance will result in the maximum conversion efficiency.[26] More specifically, at n = 4nC, the third and the fifth harmonics have conversion efficiencies of 4.65% and 0.27%, respectively.
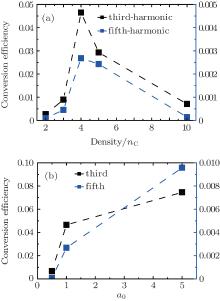 | Fig. 4. The dependences of the conversion efficiencies of the third and the fifth harmonics on (a) the plasma density and (b) the laser intensity. |
We then study the dependence of the conversion efficiency on the laser intensity a0. Figure 4(b) shows that the conversion efficiency increases as the laser intensity increases. At a0 = 5, the third and the fifth harmonics have conversion efficiencies of 7.45% and 0.96%, respectively. As the laser intensity a0 increases, the fifth harmonic conversion efficiency increases much faster than that of the third harmonic.
This simple method can be extended to generate other high-order harmonics with a specific polarization structure. In fact, we can also obtain similar results by irradiating solid targets with other ultra-intense singular beams. For example, when we use the typical RPB as the driving beam, the generated odd harmonics are also radially polarized. This selection rule for the polarization state of the generated harmonics, established for the conventional linearly polarized laser fields, [26] also holds for the vector beams with a spatial polarization modulation. On the other hand, for the normally incident vortex driving beam, our method can also be used to generate vortex harmonics with an odd topological charge due to the 2D PIC code restriction. When using the 3D PIC codes, our method can also be used for normally incident vortex driving beams with an even topological charge. That is to say, the high-order vortex harmonics will have the same helical wavefront structure as the driving field.
We have proposed the production of an intense attosecond VB train by normally irradiating a solid target with a VB driving pulse. The produced attosecond VB train, which is mainly composed of the third and the fifth harmonics, has the same vector structure as the driving pulse. Using 2D PIC simulations, we find that the conversion efficiencies of the third and the fifth harmonics reach their maxima at n = 4nC when the plasma resonates with the ponderomotive force. This method can also be applied to normally incident vortex driving beams. The realization of ultra-intense few-cycle radially polarized laser pulses[28] provides us with a new means of producing intense VBs in the extreme ultraviolet (XUV) range, and the VB has a stronger axial electric field under the sharper focus, [29] which may be used in fields such as electron acceleration with low divergence angle, nonlinear optics in the XUV region and laser-plasma diagnostics.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|



