Cite this Article
Li Yong-Qing, Zhang Yong-Jia, Zhao Jin-Feng, Zhao Mei-Yu, Ding Yong. Vector correlations study of the reaction with different collision energies and reagent vibration excitations* . Chinese Physics B, 24(11): 113402  
Permissions
Vector correlations study of the reaction with different collision energies and reagent vibration excitations*
Li Yong-Qinga),b), Zhang Yong-Jiaa), Zhao Jin-Fenga),b), Zhao Mei-Yuc), Ding Yonga)
Department of Physics, Liaoning University, Shenyang 110036, China
State Key Laboratory of Molecular Reaction Dynamics, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian 116023, China
Institute of Theoretical Simulation Chemistry, Academy of Fundamental and Interdisciplinary Sciences, Harbin Institute of Technology, Harbin 150080, China

†Corresponding author. E-mail: yqli@lnu.edu.cn

Corresponding author. E-mail: myzhao@hit.edu.cn

Corresponding author. E-mail: yongding@lnu.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant Nos. 11474141 and 11404080), the Special Fund Based Research New Technology of Methanol conversion and Coal Instead of Oil, the China Postdoctoral Science Foundation (Grant No. 2014M550158) , the Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry of China (Grant No. 2014-1685), and the Program for Liaoning Excellent Talents in University, China (Grant Nos. LJQ2015040 and LJQ2014001).

Abstract

Vector correlations of the reaction are studied based on a recent DMBE-SEC PES for the first excited state of NH2 [ J. Phys. Chem. A114 9644 (2010)] by using a quasi-classical trajectory method. The effects of collision energy and the reagent initial vibrational excitation on cross section and product polarization are investigated for v = 0–5 and j = 0 states in a wide collision energy range (10–50 kcal/mol). The integral cross section could be increased by H2 vibration excitation remarkably based on the DMBE-SEC PES. The different phenomena of differential cross sections with different collision energies and reagent vibration excitations are explained. Particularly, the NH molecules are scattered mainly in the backward hemisphere at low vibration quantum number and evolve from backward to forward direction with increasing vibration quantum number, which could be explained by the fact that the vibrational excitation enlarges the H–H distance in the entrance channel, thus enhancing the probability of collision between N atom and H atom. A further study on product polarization demonstrates that the collision energy and vibrational excitation of the reagent remarkably influence the distributions of P( θ r), P( ϕ r), and P( θ r, ϕ r).

Keyword: 34.50.Lf; 34.50.–s; 31.15.xv; vector correlations; vibrational excitation; differential cross section; stereodynamics; rotational polarization
1. Introduction

The reactivity of the nitrogen atom plays an interesting and important role in the decays of NH in pyrolysis of ammonia, atmospheric chemistry, and combustion of nitrogen containing fuels. NH2 plays a crucial role in atmospheric chemistry and combustion processes, which is also a prototype in spectroscopic and reaction dynamics studies. The ground and first excited electronic states of NH2 have been studied quite extensively by various experimental[1– 4] and theoretical techniques.[5– 32] Most investigations dealt with the potential energy surface (PES) and reaction dynamics. Among the reaction dynamics studies, most of them have dealt with the scalar properties. In order to fully understand the dynamics of the 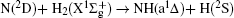reaction, it is important to study their vector properties. It can provide detailed information about the whole atoms moving when reaction occurs. With the assistance of the computational work, experimentalists can rationalize the experimental results.[31, 32] The most familiar vector correlation between the reagent and product relative velocity (k, k' ) is characterized by the differential cross section (DCS) dσ /ω t. The most important vector correlation is the correlation among three vectors k, k' , and j' (the product rotational angular momentum), which could be characterized by certain interesting double and triple vector correlations in the center-of-mass frame.

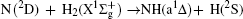
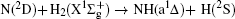
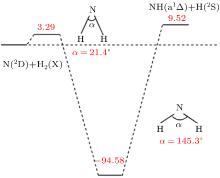
However, vector property information of the reaction based on the first excited electronic state of NH2 is very limited. In the present work, the stereodynamics of the reaction is studied based on a recent DMBE-SEC PES of the first excited state 12A′ [5] by using a quasi-classical trajectory (QCT) method, which explores the vector correlations. Five different collision energies are selected to investigate the different influences on stereodynamics with v = 0 and j = 0. Six different initial vibrational levels (v = 0– 5) are chosen to study the different effects with a collision energy of 30 kcal/mol and j = 0. The rest of this paper is organized as follows. In Section 2 we briefly review the theoretical methodologies adopted in the current study. In Section 3 we give the calculated results and discussion of the results. Finally, in Section 4 we draw some conclusions from the present study.

2. Theory
2.1. Potential energy surface

The present work is performed on the adiabatic PES reported by Li and Varandas.[5] The adiabatic PES was obtained by using double many-body expansion theory and scaled external correlation of accurate ab initio energies at the multireference configuration interaction level with the aug-cc-PVQZ basis set. The energetics of this reaction are schematically depicted in Fig. 1. All the energy levels are listed according to the corresponding entrance channels, and the DMBE-SEC PES shows a barrier of 3.29 kcal/mol along the minimum-energy path for the N(2D) + H2 reaction, before entering a well whose minimum lies about 94.58 kcal/mol deeper than the reactants, finally leading to NH(a1Δ ) + H products with an endoergicity of 9.52 kcal/mol. More details about the DMBE-SEC PES could be found in Ref. [5].

Fig. 1. Schematic of energetics (in kcal/mol) of the of DMBE-SEC PES.

2.2. Quasiclassical trajectory method

The standard QCT method has been employed to study the stereodynamics of many reactions.[33– 43] The classical Hamilton equation is numerically integrated with a six-order symplectic integration method[44] in three dimensions based on the conservation of total energy and angular momentum in each integration step of 0.1 fs to ensure that the conservations of total energy and total angular momentum are better than 10− 5 and 10− 7, respectively. Batches of 0.5 × 105 trajectories are calculated on DMBE-SEC PES for the title reaction. The orientation of the diatomic molecule and the phase of the diatomic vibrational motion are randomly sampled by the Monte Carlo procedure. Trajectories start and finish at a distance of 15 Å from the atom to the center-of-mass (CM) frame of the diatom to ensure no interaction between them.

2.3. Vector correlations

The CM frame is selected in the present work. k and k' are reactant relative velocity and product relative velocity, respectively. Vector k' is parallel to the z axis, and the y axis is perpendicular to the xz plane containing vectors k and k' . The angle between k and k' (so-called scattering angle) is denoted as θ . The polar and azimuthal angles of the final rotational angular momentum j' are represented by θ r and ϕ r, respectively.

The fully correlated CM angular distribution is written as

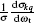
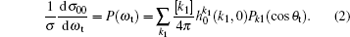
where [k] = (2k + 1), − k ≤ q ≤ k, σ is the integral cross section, is the generalized polarization dependent differential cross-section, and Ckq (θ r, ϕ r) are modified spherical harmonics. The differential cross-section (DCS) is given by

The bipolar moments are evaluated, which are equal to the expectation values of the Legendre moments of DCS, i.e., .

The k– j' angular distribution P(θ r), the most common vector correlation, is expressed in a series of Legendre polynomials as follows:

where .

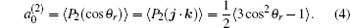
The coefficients are called orientation or alignment parameters. When k = 2, this indicates the product rotational alignment

The dihedral angular distribution function P(ϕ r) can be expanded into a Fourier series.[44] The ϕ r distribution can be written as

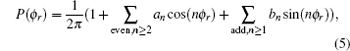where an = 2〈 cos (nϕ r)〉 and bn = 2〈 sin (nφ r)〉 . Here, the angular brackets represent an average over all the reactive trajectories.

3. Results and discussion
3.1. Integral cross section

In order to investigate the effect of the initial reagent vibration excitation on the integral cross section (ICS), figure 2 shows the ICSs with different initial reagent vibration quantum numbers at collision energies of 30, 40, and 50 kcal/mol for N + H2. It could be seen clearly that the ICSs increase with the vibration quantum number at these three collision energies, which implies that the vibration excitation of reagent has positive effects on the reactivity of the title reaction. The H2 vibration excitations can increase reaction probabilities and ICS remarkably. The enhancement effect of the vibration excitation may be attributed to the fact that this effect helps the initially H2 overcome the barrier in the entrance channel. In order to investigate the different influences on ICS with vibration quantum number at different collision energies, the ratios between the integral cross sections with different vibration quantum numbers are calculated. The ratio σ 0(v = 5)/σ 0(v = 0) at 30 kcal/mol is equal to 5.33, while the ratio at 50 kcal/mol is 4.44. It demonstrates, as can be clearly seen from Fig. 2, that the positive effect of the initial vibration on reactivity at lower collision energy seems to be more obvious than at higher collision energy.

Fig. 2. Integrated cross section for N(2D) + H2 (v = 0, j = 0– 5) as a function of v. Three kinds of lines correspond to the collision energies of 30, 40, 50 kcal/mol, respectively.

3.2. k– k' vector correlations

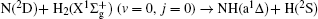
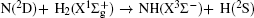
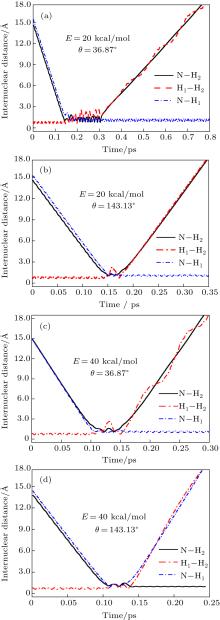
The DCS offers an excellent opportunity to study the most familiar vector correlation between the reagent and product relative velocity (k– k' ). The global k– k' angular distributions of reaction at collision energies of 10, 20, 30, 40, 50 kcal/mol based on the DMBE-SEC PES are shown in Fig. 3(a). The most remarkable feature of the angular distribution is the strong dominance of the broad forward-backward symmetry scattering. A similar forward-backward symmetry scattering of reaction of based on the ground-state PES has been reported by Pederson et al., [45] which could be comprehended easily due to the resemblant barrier and valley on reaction pathways between the ground-state PES and the lowest excited state PES (see Ref. [45]). In addition, the capture model indicates the centrifugal barrier associated with each orientation angle and then approximates the usual capture cross section by averaging over the resulting orientation-dependent maximum impact parameter.[46] Furthermore, the trajectory work of Varandas et al. suggests that classical capture models, in which the reaction is assumed to occur if the collision energy exceeds certain centrifugal barriers, yield a reasonable description of the integral cross sections, and thus rate constant.[47] Therefore, in the light of the capture model, it is easy to understand that the forward scattering increases with the increase of collision energy. The phenomenon of the strengthening of backward scattering may be attributed to an insertion reaction mechanism reported by Pino et al.[48] To study the effect of the initial reagent vibration quantum number on DCS, figure 3(b) shows the DCSs with different vibration quantum numbers at a collision energy of 30 kcal/mol. The excitation of the initial HH vibration has a great influence on k– k' angular distribution. The NH molecules are scattered mainly in the backward hemisphere at low vibration quantum number (v = 0) and evolves from backward to forward direction with increasing vibration quantum number. The vibrational excitation of HH may enhance the probability of this reaction and reaction cross section. In fact, the apparent forward scattering may be explained by the fact that the vibrational excitation enlarges the H– H distance in the entrance channel, thus enhancing the probability of collision between N atom and H atom. Therefore, if the higher vibration is excited, the more forward scattering exists. On the contrary, for the certain number of collision trajectories at each vibration quantum number qualitatively, the forward scattering increases, but the backward scattering decreases without doubt.

Fig. 3. The DCSs for the title reaction at five collision energies for different vibrational states for (a) selected collision energies of 10, 20, 30, 40, 50 kcal/mol, and (b) j = 0, v = 0, 1, 2, 3, 4, 5 for 30 kcal/mol of collision energy.

To obtain a clearer understanding of the reaction mechanism, the variations of internuclear distances of H1– H2, N– H1, and N– H2 each as a function of propagation time are shown in Fig. 4. The trajectories are selected in the scattering angle ranges of θ = 0° – 40° and 120° – 170° at 20 kcal/mol and 40 kcal/mol collision energies. Figures 4(a)– 4(d) show that the attacking atom N undergoes several collisions with the target molecule H2(H1– H2), and the complexes have relatively long lifetimes before breaking up into one of the possible channels. The long-term survival of the metastable state could allow the system to perform extensive rotations before breaking up, thereby making the products come out in more random directions. Hence, the indirect reactive trajectories, namely “ trapped” trajectories, can be observed. Therefore, it is no surprise that we observe forward and backward scattering as can be seen in Fig. 3. Specifically, figures 4(a)– 4(c) indicate that the trajectories in the scattering angle ranges are attributed to abstraction mechanism. However, when the scattering angle is θ = 143.13° , the insertion mechanism could be concluded due to the phenomenon that the ejected diatom molecule is N– H2, not N– H1. The reaction is mainly dominated by the abstraction mechanism at lower collision energies, whereas with the enhancement of collision energy, the insertion mechanism appears even though the abstraction mechanism still exists.

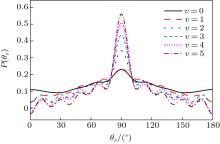
Fig. 4. Internuclear distances of H1– H2, N– H1, and N– H2 each as a function of propagation time at a collision energy of 20 kcal/mol, with scattering angle θ = 36.87° and 143.13° .

3.3. k– j' and k– k' – j' correlations on collision energy

The distributions of P(θ r) and P(ϕ r) at collision energies of 10, 20, 30, 40, 50 kcal/mol are shown in Figs. 5 and 6, which describe the k– j' correlations and k– k' – j' correlations, respectively. The maximum impact parameters bmax (Å ) calculated in collision energy range from 10 kcal/mol to 50 kcal/mol are provided in Table 1, respectively. In fact, an overall representation of the polarization of rotational angular momentum vector of the product molecular is provided in the scattering frame. The P(θ r) distribution is symmetric with respect to 90° and corresponding maximum is at 90° . The results demonstrate that j' is distributed with cylindrical symmetry in the product scattering frame and the direction of j' is perpendicular to the k direction preferentially. At low collision energies (10 and 20 kcal/mol), small peaks can be found near 15° and 165° . The peaks move to 0° and 180° with increasing collision energy (30, 40, and 50 kcal/mol). The change of the peaks indicates the influence of collision energy on the direction of j' for NH product. At low collision energy, most reactive trajectories are along the minimum energy reaction path and peaks of the P(θ r) distribution concentrate near 15° and 165° . As the collision energy increases, the more reactive trajectories are far from the minimum energy reaction path, leading to the change of the P(θ r) distribution. In addition, the peaks of P(θ r) display that the degree of the rotational alignment of the product increases with the increase of collision energy, which may be due to the expectation value of 〈 P2(cosθ r)〉 . The smaller the expectation value of 〈 P2(j' · k)〉 is, the stronger the rotational alignment could be. To show the trend in more depth, the values of 〈 P2(j' · k)〉 are calculated at collision energies from 10 to 50 kcal/mol in Table 2. In the reaction process, the total angular momentum can be conserved as L + j = j' + L' , where L and j denote the orbital angular momentum and rotational angular momentum, respectively. When the reactant rotational angular momentum is low, the equation can be expressed as L ≈ j' + L' . As the collision energy increases, the orbital angular momentum is also improved. As a result, larger parts of L are disposed into j' , which finally induces stronger alignment of j' .

Table 1. Maximum impact parameter bmax (Å ) values calculated at collision energies from 10 kcal/mol to 50 kcal/mol.
Table 2. Product rotational alignment parameter 〈 P2(j' · k)〉 values calculated at collision energies from 10 kcal/mol to 50 kcal/mol.

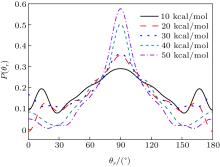Fig. 5. Distributions of P(θ r) for N + H2 (v = 0, j = 0) → NH + H at five collision energies of 10, 20, 30, 40, and 50 kcal/mol.

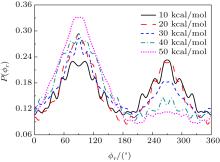Fig. 6. Distributions of P(ϕ r) for N + H2 (v = 0, j = 0) → NH + H at five different collision energies of 10, 20, 30, 40, and 50 kcal/mol from outer to inter.

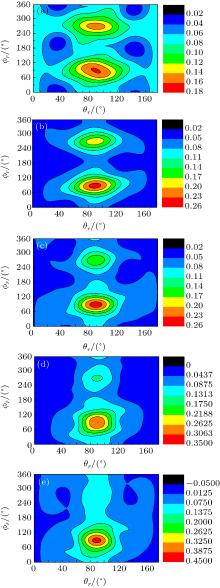
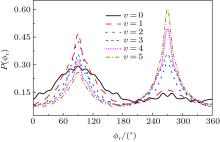
The calculated P(ϕ r) distributions of direction of j' for NH products at collision energies of 10, 20, 30, 40, and 50 kcal/mol are shown in Fig. 6, which mainly describes the k– k' – j' correlations. In all cases, these curves tend to be asymmetric with respect to k– k' scattering plane and the strong polarization of product rotational angular momentum can be reflected directly. The peaks in the P(ϕ r) distribution at ϕ r angles close to 270° imply a preference for left-handed product rotations, while the peaks at ϕ r angles close to 90° indicate a preference for right-handed product rotation. The peaks at ϕ r = 90° and 270° indicate that the rotational angular momentum vector of the products is not only aligned (the distributions have peaks at ϕ r = 90° and 270° ), but also oriented along the y axis of CM frame, which means the peaks at 90° are different from that at 270° . From Fig. 6 we can see that the peaks at 90° are stronger than that at 270° with the increase of collision energy, which implies that j' tends to be oriented along the positive direction of the y axis. It should be noted that the height of peak at 90° is equal to that at 270° when the collision energy is 10 kcal/mol, which indicates that the orientation effect of the product rotational momentum disappears, only the alignment effect exists. In turn, the peaks of P(ϕ r) distributions are broader at high collision energy, indicating that the rotation of the product NH molecular has a preference transfer from “ in-plane” to “ out-of-plane” mechanism. Such a mechanism can also be seen in Fig. 7, which shows the scattering angle average of the full distribution P(ω t, ω r) at 10– 50 kcal/mol. The peaks of the distribution of P(θ r, ϕ r) at (π /2, 3π /2), which are in good accordance with the distributions of P(θ r) and P(ϕ r).

Fig. 7. Polar plots of P(θ r, ϕ r) distribution averaged over all scattering angles at five collision energies: (a) 10 kcal/mol; (b) 20 kcal/mol; (c) 30 kcal/mol; (d) 40 kcal/mol; (e) 50 kcal/mol.

3.4. k– j' and k– k' – j' correlations on reagent vibration excitation

In this section, the role of the initial vibrational excitation in the stereodynamics is investigated. The impact parameter bmax values calculated at collision energy of 40 kcal/mol from v = 0 to v = 5 are given in Table 3. The calculated results of P(θ r) distribution for the reactions of at collision energy of 40 kcal/mol are shown in Fig. 8. It shows that the P(θ r) distribution is symmetric with respect to 90° and corresponding peaks are at 90° . It is noteworthy that P(θ r) distribution at 90° becomes somewhat narrower and higher with the increase in the vibrational quantum number, indicating that the product vibrational alignment effect becomes stronger when the reagent is in a vibrational excited state. When v > 0, several small peaks can be found on the distribution of P(θ r) except θ r = 90° . For v = 0, most reactive trajectories are along the minimum energy reaction path because of low collision energy. For vibrational excitation of the reagent, additional energy from the vibrational energy can turn into the reactive process. Therefore, more reactive trajectories are far from the minimum energy reaction path, leading to the change of P(θ r). This is also confirmed by the values of the product rotational alignment parameter 〈 P2(cosθ r)〉 shown in Table 4. It can be understood that the intermediate vibrates more intensively with the increase of vibration quantum number v, facilitating H atom to break the bondage to eject out. Thus, the stronger rotational polarization of the product may finally result in higher vibrational excited states.

Fig. 8. Distributions of P(θ r) for N + H2 → NH + H reaction (j = 0, v = 0– 5) at 40 kcal/mol.

Table 3. Maximum impact parameter bmax (Å ) values calculated at collision energy of 40 kcal/mol from v = 0 to v = 5.
Table 4. Product rotational alignment parameter 〈 P2(j' · k)〉 values calculated at collision energy of 40 kcal/mol from v = 0 to v = 5.

The calculated P(ϕ r) distributions of direction of j' for NH products at different vibration quantum numbers (v = 0– 5) are shown in Fig. 9, which shows that the curves are asymmetric with respect to the scattering plane. Two peaks at 90° and 270° demonstrate a clear preference for orientation along the y axis, manifesting that the reaction proceeds preferentially as the velocity vector is located in a plane containing all the three atoms. In turn, the peak at ϕ r = 270° is apparently stronger than that at ϕ r = 90° when v = 0, 1, 2, reflecting that j' is oriented along the negative direction of the y axis. In contrast, j' is oriented along the positive direction of the y axis when v = 3, 4, 5. Moreover, the peaks of P(ϕ r) distributions are broader at high reagent vibrational excitement, indicating that the rotation of the product NH molecular has a preference transfer from “ in-plane” to “ out-of-plane” mechanism with the increase of vibration quantum number v.

Fig. 9. dihedral angle distributions of P(ϕ r) with respect to the k– k' – j' plane for N + H2 → NH + H from inner (j = 0, v = 0) to outer (j = 0, v = 5).

4. Conclusions

In the present work, the QCT method is used to investigate the influences of collision energy and reagent vibrational excitation on integral cross section, differential cross section, and product polarization for the title reaction. Both collision energy and vibrational excitation of reagent have a positive influence on the reactivity of the title reaction. The DCS distributions are mainly forward– backward symmetry scattering with the increase of collision energy, while the DCSs evolve from backward to forward direction with increasing vibrate quantum number. Particularly, the DCSs show that the title reaction is mainly dominated by the abstraction mechanism at lower collision energy. While with the enhancement of collision energy, the insertion mechanism appears even though the abstraction mechanism still exists. In addition, the product rotational angular momentum is not only aligned but also oriented along the y axis, except when the collision energy is 10 kcal/mol, for which the orientation effect disappears and only the alignment effect remains. The peak of P(θ r) is found to be enhanced when the H2 radical is vibrationally excited, which is in good agreement with the behavior of the alignment parameter 〈 P2(j' · k)〉 . It can be concluded that not only the rotation of the product NH molecular has a preference converting from “ in plane” reaction mechanism to “ out of plane” mechanism, but also the final angular momentum is oriented along the y axis with the increase of collision energy or initial vibration excitation.

Reference
1 Umemoto H, Asai T and Kimura Y 1997 J. Chem. Phys. 106 4985 DOI:10.1063/1.473546 [Cited within:1]
2 Alagia M, Balucani N, Cartechini L, Cachavecchia P, Volpi G G, Pederson L A, Schatz G C, Lendvay G, Harding L B, Hollebeek T, Ho T S and Rabitz H 1999 J. Chem. Phys. 110 8857 DOI:10.1063/1.478806 [Cited within:1]
3 Dodd J A, Lipson S J, Flanagan D J, Blumberg W A M, Pearson J C and Green B D 1991 J. Chem. Phys. 94 4301 DOI:10.1063/1.460616 [Cited within:1]
4 Umemoto H and Matsumoto K 1996 J. Chem. Phys. 104 9640 DOI:10.1063/1.471716 [Cited within:1]
5 Li Y Q and Varand as A J C 2010 J. Phys. Chem. A 114 9644 DOI:10.1021/jp100273r [Cited within:4]
6 Takayanagui T, Kobayashi H and Tsunashima S 1996 J. Chem. Soc. Faraday Trans. 92 1311 DOI:10.1039/ft9969201311 [Cited within:1]
7 Li Y Q and Varand as A J C 2010 J. Phys. Chem. A 114 6669 [Cited within:1]
8 Pederson L, Schatz G, Hollebeek T, Ho T S, Rabitz H and Harding L B 2000 J. Phys. Chem. A 104 2301 DOI:10.1021/jp9924575 [Cited within:1]
9 Li Y Q, Ma F C and Sun M T 2013 J. Chem. Phys. 139 154305 DOI:10.1063/1.4824188 [Cited within:1]
10 Jensen P, Buenker R J, Hirsch G and Rai S N 1990 Mol. Phys. 70 443 DOI:10.1080/00268979000101111 [Cited within:1]
11 Li Y Q, Song Y Z, Song P, Li Y Z, Ding Y, Sun M T and Ma F C 2012 J. Chem. Phys. 136 194705 DOI:10.1063/1.4718705 [Cited within:1]
12 Funken K, Engels B, Peyerimhoff S D and Grein F 1990 Chem. Phys. Lett. 172 180 DOI:10.1016/0009-2614(90)87294-2 [Cited within:1]
13 Chu T S and Han K L 2005 J. Phys. Chem. A 109 2050 DOI:10.1021/jp0451391 [Cited within:1]
14 Chu T S, Han K L and Varand as A J C 2006 J. Phys. Chem. A 110 1666 DOI:10.1021/jp054572n [Cited within:1]
15 Chu T S, Zhang Y and Han K L 2006 Int. Rev. Phys. Chem. 25 201 DOI:10.1080/01442350600677929 [Cited within:1]
16 Chu T S and Han K L 2008 Phys. Chem. Chem. Phys. 10 2431 DOI:10.1039/b715180b [Cited within:1]
17 Suzuki T, Shihira Y, Sato T, Umemoto H and Tsunashima S 1993 J. Chem. Soc. Faraday Trans. 89 995 DOI:10.1039/ft9938900995 [Cited within:1]
18 Buenker R J, Peric M, Peyerimhoff S D and Marian R 1981 Mol. Phys. 43 987 DOI:10.1080/00268978100101821 [Cited within:1]
19 Li Y Q, Yuan J C, Chen M D, Ma F C and Sun M T 2013 J. Comput. Chem. 34 1686 DOI:10.1002/jcc.23310 [Cited within:1]
20 Pederson L A, Schatz G C, Ho T, Hollebeek T, Rabitz H and Harding L B 1999 J. Chem. Phys. 110 9091 DOI:10.1063/1.478830 [Cited within:1]
21 Chu T S, Lu R F, Han K L, Tang X N, Xu H F and Ng C Y 2005 J. Chem. Phys. 122 244322 DOI:10.1063/1.1948380 [Cited within:1]
22 Brand i R, Leonardi E and Petrongolo C 1997 J. Phys. Chem. A 101 5696 DOI:10.1021/jp970390k [Cited within:1]
23 Peyerimhoff S D and Buenker R J 1979 Can. J. Chem. 57 3182 DOI:10.1139/v79-521 [Cited within:1]
24 Rodrigues S P J, Fontes A C G, Li Y Q and Varand as A J C 2011 Chem. Phys. Lett. 516 17 DOI:10.1016/j.cplett.2011.09.050 [Cited within:1]
25 Adam L, Hack W, McBane G C, Zhu H, Qu Z W and Schinke R 2007 J. Chem. Phys. 126 034304 DOI:10.1063/1.2409926 [Cited within:1]
26 Qu Z, Zhu H, Schinke R, Adam L and Hack W 2005 J. Chem. Phys. 122 204313 DOI:10.1063/1.1899563 [Cited within:1]
27 Vetter R, Zülicke L, Koch A, van Dishoeck E F and Peyerimhoff S D 1996 J. Chem. Phys. 104 5558 DOI:10.1063/1.471796 [Cited within:1]
28 Zhou S L, Xie D, Lin S Y and Guo H 2008 J. Chem. Phys. 128 224316 DOI:10.1063/1.2939016 [Cited within:1]
29 Varand as A J C and Poveda L A 2006 Theor. Chem. Acc. 116 404 DOI:10.1007/s00214-006-0092-6 [Cited within:1]
30 Bella S and Schaefer H FIII 1977 J. Chem. Phys. 67 5173 DOI:10.1063/1.434692 [Cited within:1]
31 Li X, Wang M, Pino I, Yang C and Ma L 2009 Phys. Chem. Chem. Phys. 11 10438 DOI:10.1039/b913713k [Cited within:1]
32 Li X, Wang M, Pino I, Yang C and Wu J 2010 Phys. Chem. Chem. Phys. 12 7942 DOI:10.1039/b926879k [Cited within:2]
33 Liu L S and Shi Y 2011 Chin. Phys. B 20 013404 DOI:10.1088/1674-1056/20/1/013404 [Cited within:1]
34 Li Y Q, Zhao J F, Zhang Y J, Chi X L, Ding Y and Ma F C 2014 Chin. Phys. B 23 123401 DOI:10.1088/1674-1056/23/12/123401 [Cited within:1]
35 Ma J J, Zou Y and Liu H T 2013 Chin. Phys. B 22 063402 DOI:10.1088/1674-1056/22/6/063402 [Cited within:1]
36 Zhao D, Chu T S and Hao C 2013 Chin. Phys. B 22 063401 DOI:10.1088/1674-1056/22/6/063401 [Cited within:1]
37 Yu Y J and Xiu Q 2011 Chin. Phys. B 20 123402 DOI:10.1088/1674-1056/20/12/123402 [Cited within:1]
38 Han K L, He G Z and Lou N Q 1996 J. Chem. Phys. 105 8699 DOI:10.1063/1.472651 [Cited within:1]
39 Wei Q 2014 Chin. Phys. B 23 023401 DOI:10.1088/1674-1056/23/2/023401 [Cited within:1]
40 Yue X F 2013 Chin. Phys. B 22 113401 DOI:10.1088/1674-1056/22/11/113401 [Cited within:1]
41 Chi X L, Zhao J F, Zhang Y J, Ma F C and Li Y Q 2015 Chin. Phys. B 24 053401 DOI:10.1088/1674-1056/24/5/053401 [Cited within:1]
42 Han K L, Zhang L, Xu D L, He G Z and Lou N Q 2001 J. Phys. Chem. A 105 2956 DOI:10.1021/jp002181x [Cited within:1]
43 Wang Y P, Zhao M Y and Yao S H 2013 Chin. Phys. B 22 128201 DOI:10.1088/1674-1056/22/12/128201 [Cited within:1]
44 Wei L, Zhou H W and Zhang L 2013 Chin. Phys. B 22 096201 DOI:10.1088/1674-1056/22/9/096201 [Cited within:2]
45 Pederson L A, Schatz G C, Ho T, Hollebeek T, Rabitz H and Harding L B 2000 J. Phys. Chem. A 104 2301 DOI:10.1021/jp9924575 [Cited within:2]
46 Fitzcharles M S and Schatz G C 1986 J. Phys. Chem. 90 3634 DOI:10.1021/j100407a034 [Cited within:1]
47 Varand as A J C, Voronin A I, Riganelli A and Caridade P J S B 1997 Chem. Phys. Lett. 278 325 DOI:10.1016/S0009-2614(97)01005-1 [Cited within:1]
48 Pino I, Martinazzob R and Tantardini G F 2008 Phys. Chem. Chem. Phys. 10 5545 DOI:10.1039/b805750h [Cited within:1]