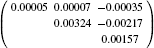Cite this Article
Megrouss Youcef, Benhalima Nadia, Bahoussi Rawia, Boukabcha Nouredine, Chouaih Abdelkader, Hamzaoui Fodil†. Determination of electrostatic parameters of a coumarin derivative compound C17H13NO3 by x-ray and density functional theory . Chinese Physics B, 24(10): 106103  
Permissions
Determination of electrostatic parameters of a coumarin derivative compound C17H13NO3 by x-ray and density functional theory
Megrouss Youcef, Benhalima Nadia, Bahoussi Rawia, Boukabcha Nouredine, Chouaih Abdelkader, Hamzaoui Fodil†
Laboratoire de Technologie et Propriétédu Solide (LTPS), University of Mostaganem, Mostaganem 27000, Algeria

†Corresponding author. E-mail: fodil hamzaoui@yahoo.fr

Abstract

This work is devoted to the experimental determination of the electrostatic properties of the molecular 4-methyl-7-(salicylidene amino) coumarin (C17H13NC3) using high resolution x-ray diffraction data. The experimental results are compared with those obtained theoretically from calculation type ab initio. The experimental investigation is carried out using the molecular electron charge density distribution based on the multipolar model of Hansen and Coppens. However the theoretical calculations are conducted by using the molecular orbital B3LYP method and the Hartree–Fock (HF) approximation with the basis set 6-31G (d,p) implemented in the Gaussian program. In addition to the structural analysis, the thermal agitation is also analyzed in terms of rigid blocks to ensure a better precision of the results. Subsequently, the electrostatic atomic and molecular properties such as the net charges, the molecular dipolar moment to highlight the nature of charge transfer existing within the molecule studied are derived. Moreover, the obtained electrostatic potential enables the localization of the electropositive and the electronegative parts of the investigated molecule. The present work reports in detail the obtained electrostatic properties of this biologically important molecule.

PACS: 61.50.–f; 61.05.cp; 31.15.A–; 31.15.ap
Keyword: electron charge density; electrostatic potential; molecular dipole moment and x-ray diffraction
1.Introduction

The coumarin derivatives have been largely investigated by many researchers for their various biological properties.[1] It has been shown that the biological activity is directly related to the configuration and the charge density distribution around the asymmetric sites of the concerned molecules.[2– 4]

In this context, the present work focuses on the study of the molecular electrostatic potential and provides some other electrostatics properties such as the net atomic charges and the molecular dipole moment. Both experimental and theoretical investigations are presented here.

The experimental investigation is based on the x-ray experiment crystal data published previously by Aazam et al.[5] In a first stage, in order to improve the accuracy of the crystallographic parameters, structural analysis and thermal motion analysis are performed using the multipolar charge density model of Hansen and Coppens[6] and the rigid-body bond test method respectively.[7] In the second stage, the obtained crystallographic multipolar parameters are used to describe the electron density distribution in the crystal.[8] The electrostatic potential around the molecule is also calculated so as to describe the nature of inter- and intra-molecular charge transfers in this compound.

The theoretical investigation consists of an ab initio molecular orbital calculation with using the Becke– Lee– Yang– Part’ s three-parameter hybrid functional (B3LYP) method and Hartree– Fock (HF) approximation with the basis set 6-31G(d, p) implemented in the Gaussian 03 package.[9] The theoretical and experimental results are compared with each other and found to be in very good agreement.

2.Crystallographic investigation
2.1.Crystal structure refinement

The crystallographic investigation described in the work of Aazam et al. is based on spherical atom refinement.[5] In order to improve the accuracy of the results and to determine the molecular charge density distribution, the Hansen-Coppens multipole formalism implemented in the Mopro least squares program for multipole refinement investigations[10] is used. The multipolar model used describes the crystal electron density as a superposition of non-spherical pseudo-atoms modeled using a multipole expansion as:

where ρ c and ρ v are spherically averaged Hartree– Fock core and valence density respectively, with ρ v being normalized to one electron; 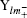are the spherical harmonic angular functions that are modulated by the Slater-type radial functions; Nl is a normalization factor. The values for parameters n = nl and ξ are chosen according to the rules suggested by Coppens (1997).[3] In practice, the expansion and contraction of the valence shell depend on two charge density variables, i.e., the population parameter and a kappa parameter; they are added to the conventional parameters of structure analysis.[5] The population parameters Pv and Plm are floated along with k′ and k″ during the refinement, the summation over m in Eq. (1) includes ± l, so that for each one, 2l + 1 functions are included. The aspheric charge density is described at the octupole level (l = 3) for the atoms C, N, and O and at the dipole levels (l = 1 or 2) for hydrogen atoms not involved and involved in strong H bonds, respectively. Charge densities of all hydrogen are considered to have cylindrical symmetry along the corresponding hydrogen– heavy atom bond.

The least-square method is used to refine the crystal structure against F2 using atomic anisotropic thermal parameters for all non-hydrogen atoms. The H atoms are located from a difference Fourier map and included in the refinement with the isotropic temperature factor of the carrier atom. After the thermal motion analysis in terms of the rigid body bond test, the anisotropic temperature factors for the hydrogen atoms are introduced. The accuracies of results are significantly improved: the final refinement R factor decreases to 0.4%. The crystallographic details are given in Table 1.

Table 1. Crystal data and structure refinement details.
Table 2. Hydrogen bonds and their properties in 4-methyl-7-(salicylideneamino)coumarin crystal.
Table 3. Atomic displacement parameters in units of Å 2.

The general feature of the structure consists of a methyl substituted coumarin group connected to a 2-hydroxyphenyl ring via an azomethine linkage as shown in Fig. 1. The coumarin and benzene ring planes form a dihedral angle of 24.0° indicating an absence of the coupling as reported in the earlier work of Aazam et al.[5]

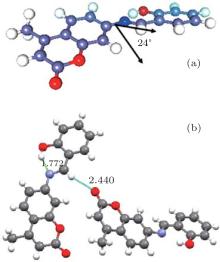Fig. 1. Chemical structures of the title compound: (a) the dihedral angle within the molecule. (b) View of the hydrogen bonding.

The exploration of the molecular environment within the unit cell gives rise to two types of interactions: the first one concerns a strong O1 … H1 … N1 intramolecular hydrogen bond and the second one involves a weak intermolecular hydrogen bond responsible for the crystal package determined by the sites C7 … C7 … C3. Table 1 gives the description of the hydrogen bonds spotted in the crystal structure.

Equivalent positions:

(i) x, y, z,

(ii) − x + 2, + y− 1/2, − z + 1/2 + 1,

(iii) x, − y− 1/2, + z + 1/2,

(iv) − x + 1, + y− 1/2, − z + 1/2.

2.2.Thermal motion analysis

The thermal motion analysis of 4-methyl-7-(salicylideneamino) coumarin is performed using the THMA11 program.[7] The rigid-body motion is described by three tensors, T for the translation, L for the liberation, and S when taking into account the correlation between translation and liberation. These tensors are obtained by a least-square fit refinement by using the observed atomic thermal motion parameters obtained from the x-ray refinement reported in Table 4. In the rigid body bond model, the bonded pairs of the non-H atoms are assumed to have differences between the mean-square displacement amplitudes (MSDAs) along the interatomic directions Δ ≤ 10.10− 4 Å 2.[8] For all pairs of atoms in the molecule, the MSDAs Δ AB in the AB direction are calculated and reported in Table 3.

Table 4. Matrix for differences in MSDA (mean square displacements of atoms): values listed are 104 MSDAs for column atom minus that for row atom.

In the general treatment of the molecular thermal motion in terms of rigid-body (TLS) the calculated anisotropic thermal parameters are given in the Trueblood notation such as:[11]

where G, and D are geometrical parameters. The last term on the right-hand side of Eq. (2) is related to any additional intra-libration (Ω ) around a chosen axis. The rigid-body fit suggests one independent liberation axis around the bond C(8)– N(1). The thermal motion of the H atoms takes into account two contributions. The first one is due to the rigid molecular motion and the second one comes from the C– H vibrations.[12, 13] The T, L, and S tensors obtained from the least-square fitting are given in Table 5. The C– H bond frequencies of the molecule are cited from Baert et al.’ s work.[14] The results of the thermal motion parameters of the H atoms are summarized in Table 6. Using the MoPro viewer diagram, [15] the ellipsoids of the different atoms representing their thermal motion described above are shown in Fig. 2.

Fig. 2. MoPro diagram: thermal ellipsoids are shown for the 50% probability level.

Table 5. Rigid body vibration parameters of the T, L, and S tensors.
Table 6. Thermal vibration parameters for the H atoms calculated from the TLS group tensors plus the internal C– H bond vibration.
3.Theoretical ab initio investigation

In order to investigate the theoretical calculations of the molecular structure parameter the ab initio methods are adopted. These calculations are performed with the density functional theory (DFT) at B3LYP (Becke’ s three-parameter hybrid functional using the correlation functional of Lee, Yang, and Parr, which includes both local and non-local terms in the correlation functional) method at the 6-31G* level using the Gaussian 03 computational chemistry program package.[9] The parameters of the optimized structure (bond lengths and bond angles) are listed in Tables 7 and 8 respectively. It has been observed that all the calculated parameters are in accordance with the x-ray results. In spite of the differences, the determined geometric parameters represent a good approximation which enables the calculation of other parameters, such as the vibrational wave numbers. It should be noted that some of the optimized bond lengths and bond angles have slightly different values from the corresponding experimental ones due to the fact that the theoretical calculations consider only isolated molecules in the gaseous phase while the experimental results refer to molecules in a crystal environment.

Table 7. Bond lengths of 4-methyl-7-(salicylideneamino) coumarin in units of Å .
Table 8. Bond angles of 4-methyl-7-(salicylideneamino) coumarin in units of (° ).
4.Results and discussion
4.1.Electron density maps

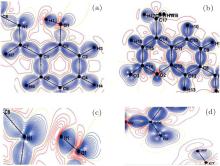
The non-spherical atom model used in multipole refinement gives structure factor phases closer to the true phases for crystals than the spherical model does. This enables the mapping of the electron density distribution by using difference Fourier synthesis to observe the experimental charge density deformation of the molecule.

Figure 3 shows the electron charge density distributions in two different planes of the molecule: the first plane (a) formed by the electro-acceptor group (2-hydroxyphenyl), and the second plane (b) containing the electro-donor group (coumarin). In these figures, one can observe the absence of the density on the atomic sites and the appearance of all the bond density peaks as expected in the literature. These maps show a first confirmation concerning the high quality of the data sets and the efficiency of the used model of Hansen and Coppens.[6]

Fig. 3. Deformation density maps with a contour interval of 0.05 eÅ − 3, positive density in blue, and negative density in red: (a) plane of the 2phenol amino, (b) the coumarin plane, (c) in the plane of intramolecular hydrogen bond N1… H1… O1, and (d) in the plane of the intermolecular hydrogen bond C7… H7… O3.

4.2.Electrostatic molecular properties

The knowledge of the analytical function of the electron density distribution produced by high resolution x-ray experiment, could give rise to some important molecular electrostatic properties such as the atomic net charges, the molecular dipole moment, and the electrostatic potential around the molecule.

4.3.Net atomic charges

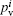
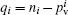
The partial charges on the different atoms are estimated by using the valence population coefficients according to the following equation where ni is the total number of electrons of atom i. The population coefficients are presented in Table 9. The refined atomic charges have the signs generally determined by the chemical knowledge: H atoms are positively charged, whereas O and N atoms are negatively charged. In Table 8 the theoretical net charges are also reported. It can be observed that experimental and theoretical results are in agreement.

Table 9. Net charges (q) in the different atoms of the title compound.
4.4.Molecular dipole moment

On the basis of the population coefficients of the multipolar density model, the molecule dipole moment could be predicted by using the following equation:

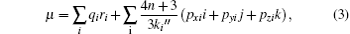
where ri is the atomic position, n the number of electrons in the molecule, and Pi are the dipolar electron populations. Dipole moment orientation in the molecule is shown in Fig. 4. There is no paradox between the resulting molecular dipole moment direction and the evaluation of the positive sign of the net charges on the H atoms and the negative sign of the net charges on O, and N atoms. The net charges on the different atoms and the molecular dipole moment are also estimated by ab initio (B3LYP/6-31G*) calculations. In this procedure the treatment is restricted to the valence– shell electrons. The results of these calculations are presented in Table 10. From the results, it is shown that the values obtained with x-ray diffraction and the values obtained by theoretical DFT calculations are in agreement. The analysis of the obtained dipole moments shows that the size and direction of the dipole moment vector depend mainly on the position of the substituent, furthermore the orientation of the dipole moment vector is oriented toward 2-hydroxyphenyl.

Fig. 4. Orientation of the molecular dipole moment of the title compound; the origin is at the center of mass of the molecule; μ exp: molecular dipole moment from the multipolar model; μ c: molecular dipole moment from the ab initio calculation.

Table 10. Components of the dipolar moment: x-ray experiment and theoretical ab initio calculations.
4.5.Electrostatic potential

As is well known, the electrostatic potential plays a very essential role in the study of the intermolecular interactions of molecular systems. From the obtained continuous charge distribution at a point defined by r′ , the potential is given by

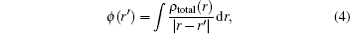
in which ρ total represents both the nuclear and the electronic charge. The integration goes over the molecular volume, and r represents the atomic position relative to a common origin.

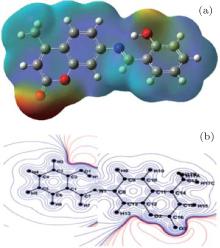
Figure 5 presents the electrostatic potential distribution around the molecule obtained from the experimental x-ray diffraction data (Fig. 5(a)) and the ab initio theoretical calculations. The obtained electrostatic potential as shown in Fig. 5 is composed of the positive electrostatic potential around the 2-hydroxyphenyl groups and the negative electrostatic potential around the coumar in the groups region. This figure also confirms the nature of the intramolecular charge transfer as determined by the orientation of the molecular dipole moment.

Fig. 5. Electrostatic potential maps around the molecule. Panel (a) shows the ab initio molecular orbital calculations of the electrostatic potential distribution, and panel (b) displays the electrostatic potential distribution predicted from the experimental x-ray diffraction data.

5.Conclusions

In this work, an accurate charge density function is determined in a high resolution crystallographic experiment. This function enables the derivation of some electrostatic molecular proprieties such as the dipole moment and the electrostatic potential on the basis of the multipolar charge density distribution model of Hansen and Coppens as is the case in many previous studies.[16, 17]

The structure refinements are achieved by using the multipolar model. All non-hydrogen atoms are refined anisotropically and are subjected to local symmetry constraints. The H atom anisotropic parameters are obtained from thermal motion analysis based on the rigid body bond test. The final reliability factor R is found to decrease until 0.4%. This very low value testifies about the quality of the used experimental data and the efficiency of the multipolar model to describe the electron density distribution in crystals.

Using the MoPro package, a variety of dynamic density deformation maps can be drawn in which the accumulation of the electron charge density along the chemical bonding is shown clearly. It is found that the electron density distribution is almost centered in the middle of the chemical bonds and the oxygen free electron pairs are perfectly localized.

The ab initio theoretical structure investigation using the Gaussian 03 package leads to an optimized molecule with bond lengths and bond angles closer to the x-ray experimental results. No significant structural changes are observed compared with the previous results. In general the theoretical electrostatic properties are in good consistence with those derived from the experiment.

Finally, the obtained results indicate the direction of charge transfer within the molecule. The deformation of the electrostatic potential of the title compound shows that the electronegative potential is located on the side of the coumarin group whereas the electropositive potential is on the side of 2-hydroxyphenyl. For a more comprehensive study of the effect of electron charge transfer in this important biological compound, it is recommended to complete the study by performing a vibrational analysis using FT-Raman and FTIR spectroscopic techniques.

Reference
1 Silva P S P, Parveen M, Khanam Z, Ali A and Silva M R 2010 Acta Cryst. E 66 o988 DOI:10.1107/S1600536810011360 [Cited within:1]
2 Nofal Z M, El-Zahar M I and El-Karim S S A 2000 Molecules 5 99 DOI:10.3390/50200099 [Cited within:1]
3 Coppens P 1997 X-ray Charge Densities and Chemical Bonding New York Oxford [Cited within:1]
4 Spackman M A 1998 Ann. Rep. Prog. Chem. C. 94 177 [Cited within:1]
5 Aazam E S, Fawazy A and Hitchcock P B 2006 Acta Cryst. E 62 o4285 [Cited within:4]
6 Hansen N K and Coppens P 1978 Acta Cryst. A 34 909 DOI:10.1107/S0567739478001886 [Cited within:2]
7 Trueblood K N 1990 Program THMAI1 Los Angeles Department of Chemistry and Biochemistry, University of California [Cited within:2]
8 Hirshfeld F L 1976 Acta Cryst. A 32 239 DOI:10.1107/S0567739476000533 [Cited within:2]
9 Frisch J, Trucks G W, Schlegel H B, Scuseria G E, Robb M A, Cheeseman J R, Montgomery J A, Vreven J T, Kudin K N, Burant J C, Millam J M, Iyengar S S, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson G A, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox J E, Hratchian H P, Cross J B, Adamo C, Jaramillo J, Gomperts R, ., Stratmann R E, Yazyev O, Austin A J, Cammi R, Pomelli C, Ochterski J W, Ayala P Y, Morokuma K, Voth G A, Salvador P, Dannenberg J J, Zakrzewski V G, Dapprich S, Daniels A D, Strain M C, Farkas O, Malick D K, Rabuck A D, Raghavachari K, Foresman J B, Ortiz J V, Cui Q, Baboul A G, Clifford S, Cioslowski J, Stefanov B B, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin R L, Fox D J, Keith T, Al-Laham M A, Peng C Y, Nanayakkara A, Challacombe M, Gill P M W, Johnson B, Chen W, Wong M W, Gonzalez C and Pople J A 2003Gaussian 03 Pittsburgh Gaussian 03 Revision A. 1 [Cited within:2]
10 Jelsch C, Guillot B, Lagoutte A and Lecomte C 2005 J. Appl. Crystallogr. 38 1 DOI:10.1107/S0021889804025518 [Cited within:1]
11 Hirshfeld F L 1971 Acta Cryst. B 27 769 DOI:10.1107/S0567740871002905 [Cited within:1]
12 Hirshfeld F L 1977 Theor. Chim Acta 44 129 DOI:10.1007/BF00549096 [Cited within:1]
13 Hirshfeld F L and Hope H 1980 Acta Cryst. B 36 406 DOI:10.1107/S0567740880003366 [Cited within:1]
14 Baert F, Schweiss P, Heger G and More M 1988 J. Mol. Struct. 178 29 DOI:10.1016/0022-2860(88)85003-8 [Cited within:1]
15 Guillot B 2011 Acta Cryst. A 67 C511 DOI:10.1107/S0108767312016571 [Cited within:1]
16 Drissi M, Chouaih A, Megrouss Y and Hamzaoui F 2013 Journal of Crystallography 2013 ID 326457 DOI:10.1155/2013/326457 [Cited within:1]
17 Boubegra N, Chouaih A, Drissi M and Hamzaoui F 2014 Chin. Phys. B 23 016103 DOI:10.1088/1674-1056/23/1/016103 [Cited within:1]